علمِ ریاضی: حقیقت کا عکس یا خود ایک حقیقت؟

نیپچُون سیارے کے بارے میں سوچیے۔

کیوں؟

کیونکہ پہلی نظر میں تو یہ سیارہ نظر ہی نہیں آئے گا۔

ایک اچھی بھلی دوربین سے بھی نظر نہیں آئے گا۔

کرّۂِ ارض سے چار ارب تیس کروڑ کلومیٹر دور واقع، نظامِ شمسی کا یہ آٹھواں سیارہ، دور کہیں آسمان میں ایک چھوٹا سا سفید رنگ کا ایک نقطہ لگتا ہے۔

یہی وجہ ہے کہ زمین سے زُہرہ یا مریخ جیسے قریب سیاروں نے جو ہمیں پوری چمک دمک کے ساتھ نظر آتے ہیں، انھوں نے ہمارے ذہن کو صدیوں سے ورطۂ حیرت میں ڈالا ہوا ہے۔

اس کے برعکس، ہم نیپچون کے وجود سے حال ہی میں، یعنی 19ویں صدی میں آگاہ ہوئے۔

اس سیارے کی دریافت دو لحاظ سے اہم ہے۔

یورینس اور نیپچُون

یہ صرف اتنی بات نہیں تھی کہ ہمیں کوئی نیا ہمسایہ مل گیا تھا۔ یونیورسٹی کالج آف لندن میں خلائی سائنس کے ماہر اور ملرڈ سائنس لیباریٹری کی لوسی گرین کہتی ہیں کہ ’نیپچون کی دریافت نے نظام شمسی میں تلاش کے سفر میں اضافہ کیا، کیونکہ اس کی دریافت ایسے نہیں ہوئی کہ ہم آسمان میں اپنی آنکھ کے ذریعے یا دور بین کی مدد سے کسی شے کو تلاش کر رہے تھے اور یہ دریافت ہو گیا۔‘

نیپچون ریاضی کی بدولت دریافت ہوا تھا۔

19ویں صدی میں، نیوٹن کے قانونِ ثقل کے بارے میں خاصی آگاہی ہو چکی تھی اور اس کی وجہ سے نظام شمسی کے سیاروں کے مداروں کا تعین کیا جا سکتا تھا، سوائے یورینیس کے جس کا مدار دوسرے سیاروں کی نسبت اپنے متوقع مدار سے ذرا سا سِرکا ہوا تھا۔

اُس وقت یہ سورج سے سب سے زیادہ فاصلے پر واقع سیارہ سمجھا جاتا تھا اور کچھ ماہرین کے مطابق شاید اتنے زیادہ فاصلے پر نیوٹن کا قانون اتنا موثرنہ ہو۔

لیکن دوسرے ماہرین نے علمِ ریاضی پر انحصار کرتے ہوئے حساب و کتاب کے بعد سوچا کہ خلا کے اُس مقام پر کوئی اور شے ہونی چاہئیے جو سورج کے ارد گرد یورینس کے مدار کو تبدیل کر رہی ہے۔

لوسی گرین کہتی ہیں کہ ’انھوں (ریاضی دانوں) نے حساب کتاب لگانا شروع کیا کہ یہ شے کہاں ہے اور یہ کیسے وہاں پر موجود ہے؟ اور پھر جب انھوں نے ریاضی کی نشاندہی والے خلائی مقام کی جانب اپنی طاقتور دوربین کا رُخ کیا تو انھوں نے یہ نیا سیارہ دریافت کر لیا۔‘

نیپچون کی دریافت نے تاریخی طور پر یہ ثابت کیا ہے کہ ریاضی ایک دریافت شدہ علم نہیں ہے بلکہ ریاضی کا اپنا ایک وجود ہے۔

اور اسی خیال نے بی بی سی کراؤڈ سائنس پروگرام کے پیرو سے تعلق رکھنے والے ایک سامع سرگیو ہوارکیا کے ذہن میں کئی سوالات پیدا کیے۔

وہ لکھتے ہیں کہ ’گلیلیو، جو کہ ایک ڈھلوان سے لڑھکتی ہوئی ایک گیند کی رفتار بتا سکتا تھا، ان سے لے کر علم طبیعات کے بنیادی ذرّے کے بارے میں ہِگس کے فیلڈ تک، جس کی پیشنگوئی علوم ریاضی کے ماہرین نے اس کی دریافت سے پہلے کردی تھی، کسی شے کے معلوم ہونے سے پہلے اس کے وجود کے ہونے کی پیشنگوئی کرنے کی یہ صلاحیت مجھے بہت حیران کرتی ہے۔‘

’کیا علم ریاضی ایک ماڈل ہے، ایک بیان ہے، حقیقت کا ایک استعارہ ہے، یا خود اپنی حیثیت میں ایک حقیقت ہے؟‘

ایسے سوالات اٹھانے والے صرف سرگیو ہی نہیں ہے۔ فلسفی اس خیال پر ہزاروں برسوں سے غور کرتے رہے ہیں۔

اور یہ سوال کئی بنیادی اختلافات کا سبب بنا رہا ہے۔

یہ منفی کیک نہیں ہے

یہ بات اب یقینی طور پر کہی جاسکتی ہے کہ انسان نے ریاضی سے کھیلنے کا کام اپنی ضروریات کی وجہ سے شروع کیا، مثلاً اشیاء کو گننا یا ان کی پیمائیش کرنا۔ تو پھر چلیے یہیں سے شروع کرتے ہیں۔

اور چلیے اس کے لیے کیک کو ایک مثال کے طور پر لیتے ہیں۔

علم ریاضی ہمیں ایک کیک کے بارے ہر بات بتا سکتا ہے۔ اس کی لمبائی چوڑائی کیا ہے، اس کا وزن کیا ہے، اسے کس طرح تقسیم کرنا ہے۔ یہ سب ٹھوس معلومات ہیں۔

اور ہمیں کیک یہ دکھا سکتا ہے کہ علم ریاضی وہ وہ باتیں بھی بتا سکتا ہے جن کے بارے میں بظاہر حقیقی علم نہیں بتا سکتا ہے۔

اگر آپ کیک کا ایک تہائی حصہ کھا لیں تو باقی دوتہائی حصہ رہ جاتا ہے۔

چلیں یہ تو سمجھ میں آتا ہے۔ اور اگر آپ تیسرا ایک تہائی حصہ کھا لیں تو پھر باقی کچھ نہیں بچتا ہے۔

ریاضی کی کتابوں کے مصنف ایلیکس بیلوز کہتے ہیں کہ ’ہم ایک قدیمی بات کے ذہنی محیط کو بیان کر رہے ہیں۔‘

وہ لوگ عملی ریاضی کے ذریعے پیمائیش کرتے تھے اور گنتے تھے۔ اور ان کے لیے منفی اعداد کا وجود نہیں تھا۔

اگر آپ کے ذہن میں کسی شے کا وجود صرف یہ ہو کہ اسے گنا جاستکا ہے یا اس کی پیمائیش کی جاسکتی ہے تو پھر آپ کے لیے یہ تصور کرنا کافی مشکل ہو گا کہ کوئی شے صفر سے بھی کم ہو سکتی ہے۔

قرضے اور منفی اعداد

آپ جیسے ہی کیک کا بچا کُھچا حصہ بھی کھا لیتے ہیں تو وہ ختم ہو جاتا ہے۔ لہٰذا کیک منفی عدد کی صورت میں وجود نہیں رکھتا ہے۔

لیکن بیلوز کہتے ہیں کہ یہ ایک ایسا میدان ہے جہاں آپ منفی اعداد کا استعمال کرتے ہیں اور یہ ایک قدرتی اور معمول کا کام ہے۔

بیلوز دولت کی مثال دیتے ہیں: ’آپ کے پاس رقم ہوتی ہے اور آپ نے کسی کو رقم دینی بھی ہوتی ہے۔‘

’پہلے منفی اعداد کا عملی استعمال اکاؤنٹس اور قرضوں میں ہوتا تھا۔‘

اگر آپ کو مجھے پانچ ڈالر دینا ہیں اور میں آپ کو پانچ ڈالرز دیتا ہوں تو آپ کے پاس صفر رقم ہے۔

یہ ایک حقیقت ہے اور یہاں سے منفی اعداد کا آغاز ہوتا ہے۔

آج کے دور میں منفی اعداد کے بغیر سوچنا بھی ناممکن ہے۔ اور یہ بات صرف قرضوں ہی تک محدود نہیں ہے۔

اب تک تو ہم حقیقت پر بات کر رہے ہیں۔

لیکن جب آپ منفی اعداد کے ساتھ کھیلنا شروع کرتے ہیں تو کچھ عجیب و غریب باتیں ہوتی ہیں۔

زبردست معمہ

اگر آپ دو اعداد کو ضرب دیں تو جواب مثبت عدد میں آئے گا۔

لہٰذا -1 x -1 = -1 اور اس وجہ سے ایک نیا معمہ پیدا ہوتا ہے۔

’اگر آپ اس مساوات کے اس کھیل کو کھیلنا شروع کریں گے جن میں منفی اعداد بھی ہیں اور مثبت اعداد بھی تو پھر آپ کو ایک اور صورت حال کا سامنا کرنا پڑے گا۔‘

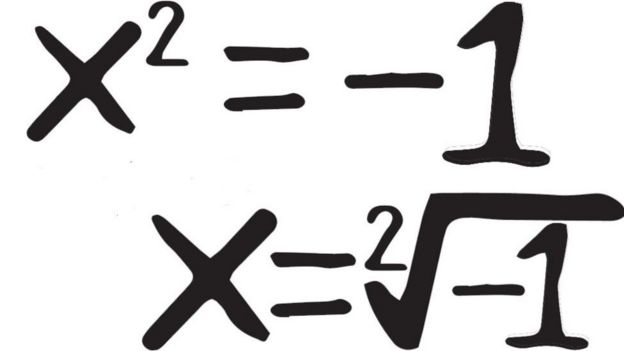
بیلوز وضاحت کرتے ہوئے کہتے ہیں کہ ’یہ کیا مصیبت ہے؟ آپ اُس عدد کو کس طرح سمجھ پائیں گے جو منفی 1 کے مربع یا سکوائیر روٹ کے برابر ہے!‘

یہ ایک مثبت عدد نہیں ہو سکتا ہے۔ کیونکہ جب آپ اُسے سکوائیر بناتے ہیں یا اُسے اُسی عدد کے ساتھ ضرب دیتے ہیں تو اس کا جواب مثبت عدد نکلتا ہے۔ اور اسی وجہ سے وہ ایک منفی عدد نہیں ہو سکتا ہے۔‘

’جب پہلی مرتبہ یہ نتیجہ نکلا تھا تو لوگوں نے اسے بے معنی سمجھا تھا۔‘

لیکن آہستہ آہستہ ریاضی دانوں نے بتایا کہ ’ہاں یہ بے معنی ہے، لیکن جب میں اسے اپنی شماریات میں استعمال کرتا ہوں تو مجھے صحیح جواب ملتا ہے۔ چلیں اس بات کو ہم فلسفیوں پر چھوڑ دیتے ہیں کہ یہ کیا ہو سکتا ہے۔ ہم ریاضی دانوں کو جوابات چاہئیے ہوتے ہیں، اور اگر یہ بات ہمیں اس میں مدد دیتی ہے تو ٹھیک ہے۔‘

اور اس طرح ہمیں محض حقیقت ملتی ہے۔

لیکن جو بھی بات ہو، ریاضی پھر بھی اس کی وضاحت فراہم کرنے میں استعمال ہوتی ہے۔

خیالی یا فرضی

بیلوز کہتے ہیں کہ ’منفی 1 کی سکوائیر روٹ کو ایک خیالی یا فرضی عدد کہا جاتا ہے جو کہ ایک ہولناک عدد ہے کیونکہ اس سے یہ تاثر ملتا ہے کہ علمِ ریاضی ایک حقیقت ہے اور یہ اچانک ایک خیالی علم بن گیا۔‘

وہ کہتے ہیں کہ ’جی نہیں، علم ریاضی ابتدا ہی سے ایک خیالی علم ہے۔ ہم تین کیکوں کے بارے میں بات کرسکتے ہیں، لیکن جو ہم دیکھ رہے ہیں وہ کیک ہیں۔ ہم تین کا ہندسہ نہیں دیکھ رہے ہیں، ہم کیک ہی دیکھ رہے ہیں۔ تین کا ہندسہ ایک تجریدی فہم ہے۔

’یہ بالکل اسی طرح ہے جیسے کہ خیالی اعداد ہوتے ہیں۔ یہ سب کچھ بہت زیادہ خبتی سا لگتا ہے، لیکن اگر آپ ایک بار سمجھنا شروع کردیں کہ یہ کیسے کام کرتے ہیں تو یہ سب کچھ بہت منطقی لگنے لگتا ہے۔ اور یہ اعداد جنھیں ہم حقیقی اعداد کہتے ہیں جب یہ خیالی یا فرضی اعداد کے ساتھ رابطے میں آتے ہیں یا کام کرتے ہیں یعنی جنھیں ہم پیچیدہ اعداد (کامپلیکس نمبرز) کہتے ہیں، تو یہ ایک شاندار قسم کا بیان بن جاتا ہے جس کی مدد سے ایک گردش یا حرکت بیان کی جاتی ہے۔‘

آج کل منفی ایک کا سکوائیر روٹ ایسی ہی حقیقت ہے جتنی کہ منفی ایک کی اپنی حقیقیت بنتی ہے ’چاہے اسے ہمارے لیے سمجھنا کتنا ہی مشکل کیوں نہ ہو، جیسا کہ کسی زمانے میں ہمارے بزرگوں کے لیے منفی ایک کو سمجھنا مشکل تھا۔‘

پریشان ہونے کی ضرورت نہیں

اگر آپ اس گورکھ دھندے میں گم ہو گئے ہیں تو پریشان ہونے کی ضرورت نہیں ہے۔ اس مضمون کو پڑھتے رہیں، آپ پر سب کچھ واشگاف ہوجائے گا۔ واقعی۔

پیچیدہ اعداد یا ’کامپلیکس نمبرز‘ ایسی مساوات کے حل پیش کرتے ہیں جن کا حقیقی اعداد کے ذریعے حل نکالنا ممکن نہیں ہوتا ہے۔

یہ حقیقت کو سمجھنے کے لیے بہت ہی مددگار ثابت ہوتے ہیں اور ایسے کسی بھی معمہ کو سمجھنے کے آلۂِ کار ثابت ہوتے ہیں جن میں گردش یا لہروں کا عمل ہو۔

انہیں برقی انجینئیرنگ، ریڈار، میڈیکل عکس وغیرہ میں استعمال کیا جاتا اور یہ ایٹم کے چھوٹے حصے کے رویے کو سمجھنے میں مدد دیتے ہیں۔

لیکن یہ کیسے ہو سکتا ہے کہ ایک بات جو عمل ریاضی میں پہلے صرف ایک خواب تھا اور اب دنیا میں اتنی زیادہ اہمیت اختیار کرگیا ہے۔

کچھ لوگوں کے لیے ہنگری کے بیسویں صدی کے سائنسدان یوجین ونگر کا ہونا ایک معجزے سے کم نہیں تھا۔

ونگر نے ان ’کامپلیکس نمبرز‘ کو سنہ 1960 میں لکھے گئے اپنے ایک بہت ہی اثر انگیز مقالے میں پیش کیا تھا۔ اس مقالے کا نام تھا ’علم طبیعات میں ریاضی کی غیر معقولی موثریت کا دخل‘۔

نامعقولیت کی اثر انگیزی

تاہم اگر ریاضی کو حقیقت کو بیان کرنے کے لیے بنایا گیا ہے تو کیا یہ کہنا منطقی نہیں ہو گا کہ یہ ڈیزائن یہی کام تو سرانجام دیتا ہے؟ اس میں نامعقولیت کی بات کیا ہے؟

چلیں کسی ایسے شخص سے بات کریں جو فلسفے اور ریاضی کے میدانوں میں گہرا علم رکھتا ہے، طبیعات کے فلسفے کی ماہر، ایلینور نوکس۔

وہ کہتی ہیں کہ ’یہ درست ہے کہ اگر ہم نے علم ریاضی کو دریافت ہی اسی لیے کیا ہے کہ اس سے جسمانی یا ٹھوس نظاموں کی ہئیت کو سمجھنے میں مدد ملتی ہے تو یہ کہنا بھی منطقی ہو گا کہ اس علم کو یہی کام کرنا چاہئیے۔‘

کئی ایک ایسے معمے ہیں جنھیں حل کرنے کے لیے ریاضی دانوں نے کام کیا کیونکہ وہ ان کے حل کرنے میں دلچسپی رکھتے تھے، اور ان کی کوششوں سے وہی حل نکل آیا جس کی انھیں آنے والے وقتوں میں طبیعات میں تحقیق اور نئی دریافت کے لیے بہت زیادہ ضرورت پڑی۔

ایلینور نوکس 19ویں صدی میں ریاضی دانوں کی جیومیٹری میں دلچسپی رکھنے کی وجہ سے کیے جانے والے علم کا حوالہ دیتے ہوئے کہتی ہیں کہ ’اس کی سب سے مشہور مثال یوکلیڈین جیومیٹری ہے۔‘

’اس وقت یہ سوچا جاتا تھا کہ ہماری ساری دنیا کو یوکلیڈین جیومیٹری کے ذریعے بیان کیا جاسکتا ہے، جو کہ اب سکول کی سطح پر پڑھائی جاتی ہے۔ مثال کے طور پر قائمہ زاویۂ اصول یعنی یہ کہ ایک تکون کے تینوں زاویوں کا کل حاصل 180 ڈگری ہوتا ہے۔‘

انیسویں صدی کے ریاضی دان یوکلیڈین جیومیٹری کو غلط ثابت کرنے کے چکروں میں نہیں تھے۔ وہ صرف ایک چیز جاننے کی کوشش کر رہے تھے اور پھر انھوں نے وہ چیز دریافت بھی کرلیے یعنی ریاضیات کے دلچسپ ڈھانچے۔

نوکس کہتی ہیں کہ 20ویں صدی میں جب ایلبرٹ آئنسٹائین کو اپنے نظریۂ اضافیت سے متعلق خلاء اور وقت کے اصولوں کو بیان کرنے کی ضرورت پڑی تو انہیں نان یوکلیڈین جیومیٹری سے مدد ملی، وہ اس کے بغیر کامیاب نہیں ہوسکتے تھے۔‘

آج کل ہم سمجھتے ہیں کہ دنیا جیومیٹری کا ایک ڈھانچہ ہے جو کبھی بہت حیران کن بات سمجھی جاتی تھی، لیکن جن جن ریاضی دانوں نے اس جیومیٹری پر تحقیقی کام کیا ان میں کسی نے بھی یہ پیشنگوئی نہیں کی تھی کہ ان کے کام کی وجہ سے کیا کچھ دریافت ہو جائے گا۔

اس طرح کی پیشرفت ہمیں یہ سوچنے کے لیے تیار کرتی ہیں کہ، چاہے معجزانہ طور پر نہ سہی، ریاضی اور حقیقت کا رشتہ حیران کُن ہے۔

بنیادی حقیقت

اب جس طرح جدید طبیعات میں پیشرفت ہو رہی ہے، ہم جیسے عام لوگوں کے لیے یہ مشکل ہوتا جا رہا ہے کہ وہ ریاضی کے انتہائی پیچیدہ معاملات اور اس حقیقیت کو جسے یہ بیان کرتے ہیں، اُسے سمجھ پائیں۔

لیکن شاید یہ کوئی حیران کن بات نہیں ہے کیونکہ روز مرہ کی حقیقتیں جن کا ہم عام طور پر ہم اپنے اعضائے خمسہ سے ادراک کرتے ہیں، وہ دراصل کائنات کی بنیادی حقیقیت ہے۔

لیکن جو حیرانی والی بات ہے وہ یہ ہے کہ ریاضی ہمارے اپنے اعضائے خمسہ سے بھی بڑھ کر ہمارے ادراک کو ممکن بنا دیتی ہے۔

تاہم اس بنیادی حقیقت کی تلاش میں کیا ایسا ہوگا کہ ریاضی اس حد تک پہنچ جائے جہاں یہ پیچیدہ باتوں کو بیان کرسکے؟

ایلینور نوکس کہتی ہیں کہ ’20ویں صدی نے ہمیں آج کے دور کے دو بہت اہم نظریات دیے ہیں: کوانٹم آف مکینِکس (جس میں ایٹم یا سب ایٹم کی سطح کا بیان) اور (آئنسٹائین کا) نظریہ اضافیت۔‘

’اس بات کا بعد میں انکشاف ہوا کہ ان دونوں نظریات کی ریاضی کو ایک دوسرے کے ساتھ ملا کر دیکھنا ناقابلِ یقین حد تک پیچیدہ عمل ہے۔‘

نوکس مزید کہتی ہیں کہ کہ ہمارے پاس کوئی ایک مربوت نظام نہیں ہے جس کے ذریعے ہم یہ سمجھ سکیں کہ یہ دو نظریات باہمی طور پر کیسے ایک ساتھ رہتے ہیں۔ یہ دو نظریات ایک ہی حقیقت کو کیسے بیان کرسکتے ہیں؟‘

’مثال کے طور پر آپ کو حیرت انگیز حد تک کی سطح کی پیچیدگی کا اپنی سوچ اور اپنے مشاہدات کے درمیان ربط بنانے کا سامنا ہوتا ہے۔‘

بہرحال جیسا کہ ہم نے پہلے دیکھا ہے، اب اس میں بہت کچھ پیش رفت ہوچکی ہے: ایک خیال جو اپنے عملی فائدے کی تلاش میں ہے۔

لیکن شاید ہم اپنے اس سفر کی حد تک پہنچ چکے ہیں؟

ایلینور نوکس کہتی ہیں کہ ’اس نکتے پر شاید یہ بھی نتیجہ نکلے کہ اب تک ہم بہت زیادہ خوش قسمت رہے ہیں کہ ریاضی ہماری کائنات کو بیان کرسکتی ہے۔‘

’ایک اور پہلو یہ نکل سکتا ہے کہ ریاضی ہماری کائنات کے چیدہ چیدہ حصوں کو بیان کرسکتی ہے نہ کہ کائنات کو مکمل ایک مظہر کے طور پر۔‘

’یا پھر دنیا کو ایک مکمل مظہر کی طرح سمجھنا ہی ایک انتہائی پیچیدہ عمل ہے۔‘

نوکس کہتی ہیں کہ ’یا ہمارے لیے ریاضی ایک بلا کی طرح بہت ہی پیچیدہ علم ہے، یا یہ کہ ہم ابھی تک اس علم کو مکمل طور پر سمجھ ہی نہیں پائے اور کبھی کسی اگلے مرحلے پر سمجھ پائیں گے۔‘

ایک بہت بڑا فرق

شاید یہ سن کر ہمیں حیرانی نہ ہو کے ریاضی کے قوانی کو ٹھوس حقیقت سے ملتے ہوئے قوانین بنانا بہت ہی مشکل کام ہے۔ آخر یہ دو جہتیں ایک جیسی تو نہیں ہیں۔

جیسا کہ آئنسٹائین نے کہا تھا کہ ’ہم جتنا زیادہ حقیقت کا رخ کریں گے، اتنے زیادہ ریاضی کے پیچیدہ قوانین بنیں گے۔ اور ان کا جتنا زیادہ تیقن ہو گا وہ اتنا ہی کم حقیقت کا رخ کریں گے۔‘

ایلینور نوکس کہتی ہیں کہ ’ریاضی کی ایک خاص صفت ہے: یہ مطلقاً صحیح ہے یا غلط ہے۔ اگر کسی بات کو ریاضی کے ذریعے درست ثابت کردیا جائے تو اس نتیجے پر کوئی شک نہیں کرے گا۔‘

’طبیعات کے قوانین ایسے نہیں ہیں۔ یہ بات انھیں باقی قوانین سے ممتاز کرتی ہے۔‘

طبیعات کے ایک فلسفی کہتے ہیں ’ہم اکثر اپنے قوانین کے بارے میں غلط ثابت ہوتے ہیں۔ نیوٹن کے قوانین بہت خوبصورت ہیں، ان کا احترام بھی اور بعض صورتوں میں اب بھی درست ثابت ہوتے ہیں لیکن یہ اب مکمل طور پر درست نہیں ہوتے ہیں۔اس میں کوئی شک نہیں ہے کہ مستقبل میں یہ ثابت ہو گا کہ آئنسٹائین کا قانون بھی تقریباً ہے (مطلق درست نہیں ہے)۔‘

دریافت ہوا یا ایجاد کیا گیا

ریاضی کے خیالات کہاں سے آتے ہیں؟

یہ سوال ہر ریاضی دان کے لیے ہے۔

یوجینیا چینگ شکاگو کے سکول آف آرٹ انسٹی ٹیوٹ سے منسلک سائنسدان ہیں۔

وہ اس سوال کا جواب دے سکتی ہیں کہ ریاضی کے علم کو دریافت کہا جا سکتا ہے یا ایک ایجاد۔

’میں حقیقی طور سمجھتی ہوں کہ میں تصورات دریافت کرتی ہوں اور ان کے لیے رستے ایجاد کرتی ہوں۔ جب میں تجریدی خیالات پر تحقیق کر رہی ہوتی ہوں تو میں محسوس کرتی ہوں کہ جیسے میں ایک گھنے جنگل میں اشیا کی تلاش میں دگرگوں پھر رہی ہوں اور پھر میں اس تجریدی خیال کو ایک نظریے کے طور پر بیان کرنے کا ایک ایک رستہ تلاش کرلیتی ہوں لہٰذا اس طرح میں اپنی سوچ کے عمل کو منظم کرکے بیان کرنے کے قابل ہوجاتی ہوں۔‘

چینگ ’کیٹیگرو تھیوری‘ کے شعبے میں کام کرتی ہیں جسے ریاضی کی بھی ریاضی کہا جا سکتا ہے اور یہ ریاضی کے مختلف شعبوں کے درمیان ایک رابطہ بنانے کا کام ہے۔

ویسے حقیقت ہے کیا؟

تجریدی معاملے پر سوچنا ایک بہت ہی مشکل کام ہے، لہٰذا ہم اُن سے یہ جاننے کی کوشش کرتے ہیں کہ کیا وہ ریاضی کو ایک ایسا علم سمجھتی ہیں جو حقیقت کا مطالعہ کرتا ہے۔

’جب لوگ مجھ سے حقیقت کے بارے میں پوچھتے ہیں تو میں یہ جواب دینا چاہتی ہوں کہ ویسے حقیقت کیا ہے؟‘

’جن باتوں کو ہم حقیقت کہتے ہیں وہ تو فریبِ نظر ہیں، جن کے بارے میں ہم سوچ لیتے ہیں کہ یہ حقیقت ہیں کیونکہ ہم سب ان کا ایک ہی طرح کا ادراک کرتے ہیں۔‘

چینگ کا کہنا ہے کہ ’لوگ کہتے ہیں کہ اعداد حقیقت نہیں ہیں کیونکہ آپ انھیں چُھو نہیں سکتے ہیں۔ لیکن اس دنیا میں بہت ساری ایسی اشیاء ہیں جو حقیقت ہیں مگر آپ انھیں چھو نہیں سکتے ہیں، مثلاً بھوک۔

’اسی لیے میری ترجیح ہوتی ہے کہ میں ٹھوس اشیاء پر بات کروں، وہ اشیا جنھیں ہم چھو سکتے ہیں اور جن سے ہم براہِ راست گفت و شنید کرسکتے ہیں یا جو ہم پر اثر ڈالتی ہیں اور ہم ان پر اثر انداز ہوتے ہیں۔ اور تجریدی باتیں وہ ہیں جن سے ہمارا رابطہ صرف ذہن میں ہوسکتا ہے۔‘

’ریاضی ایک تجریدی خیال ہے لیکن دیگر اشیا کی طرح حقیقت بھی ہوسکتا ہے۔‘

حقیقت کیا ہے؟

ایک طرف تو یہ کہا جاسکتا ہے کہ ریاضی ایک حقیقت ہے۔

مثال کے طور پر، علمِ حیاتیات پر سوچیے جو کہ علم کیمیا کی بنیاد پر بنا ہوا ہے، اور اس پر اصل میں طبیعات کے قوانین کا اطلاق ہو رہا ہوتا ہے ۔۔۔۔ اور اس طرح ہم اعداد تک پہنچتے ہیں۔

یا پھر آپ نیلے آسمان کے بارے میں سوچیے جس کی وضاحت روشنی کی لہروں کے طول سے کی جاتی ہے، اور یہ سب کچھ اعداد ہیں۔

جب آپ جتنی زیادہ گہرائی میں جائیں گے تو ایسا لگے گا کہ ٹھوس حقیقت ہی ریاضی ہے۔

تاہم علم ریاضی انسانی زندگی کی ان باتوں کے بارے میں کچھ بتانے سے قاصر نظر آتا ہے جن کی بہت اہمیت ہوتی ہے، مثلاً محبت، بھوک یا اخلاقیات۔

اس لیے اتنے سارے بڑے بڑے سوالات میں سے ہم ایک سوال کا جواب یقین کے ساتھ دے سکتے ہیں: شاید ہم بی بی سی کو پیرو سے بھیجے گئے سرگیو ہوارکیا کے سوال کا حتمی جواب نہ ڈھونڈ سکیں۔

اب ہم یہ بات کہہ سکتے ہیں کہ ہم یہ جوابات یقینی طور نہیں ڈھونڈ سکیں گے۔

لیکن اس کے باوجود ان جوابات کو تلاش کرنا ایک اچھی کوشش تھی۔